Processing - Structure - Property Relationships

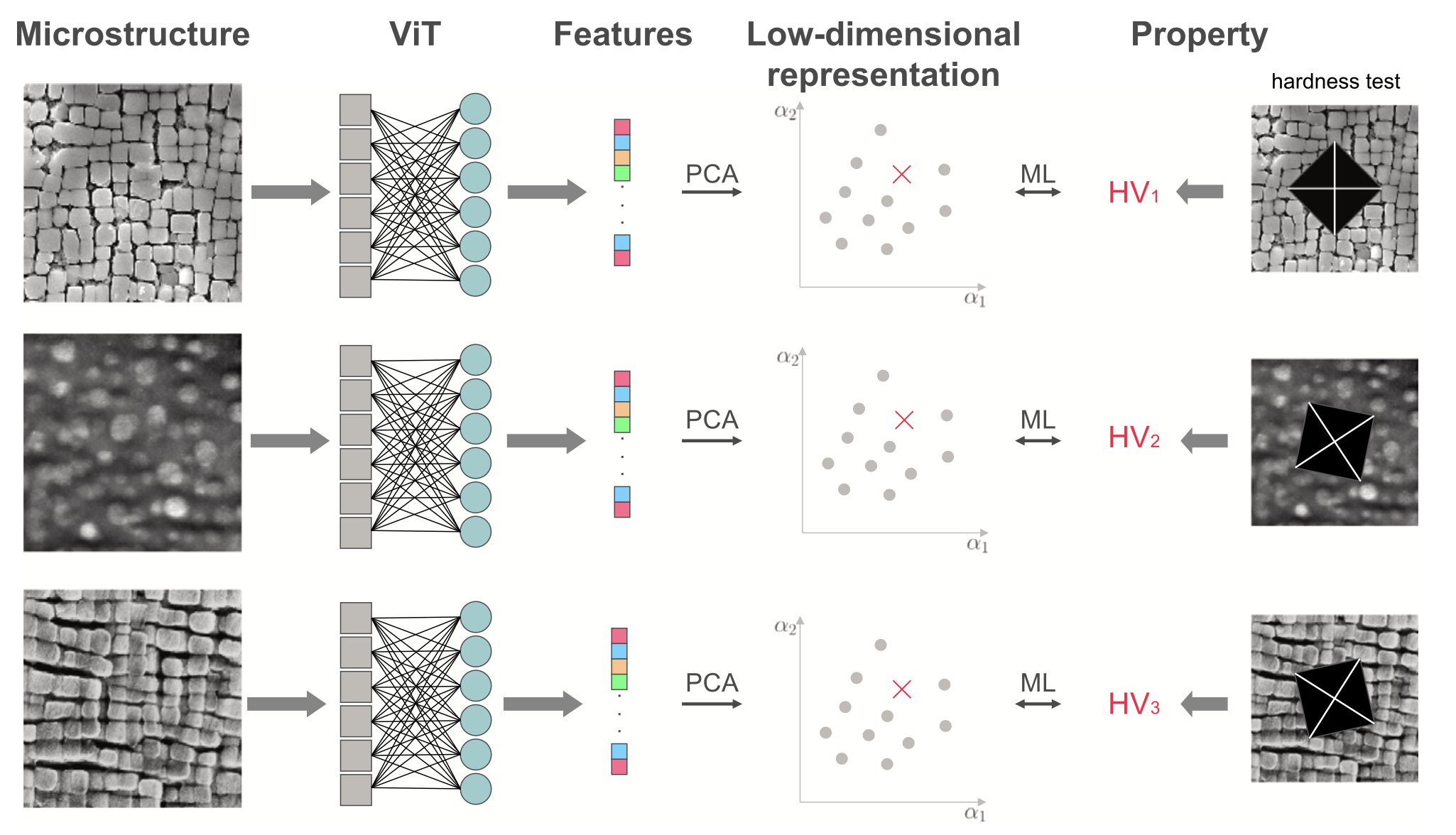
I am exploring the use of vision transformers (ViTs) and text encoders to model processing–structure–property (PSP) relationships in materials. By integrating multimodal representations from microstructure images and textual process data, this approach aims to enable more accurate and generalizable predictions of material properties without the need for fine-tuning or segmentation.

Spatially-Resolved Chord Length Distributions

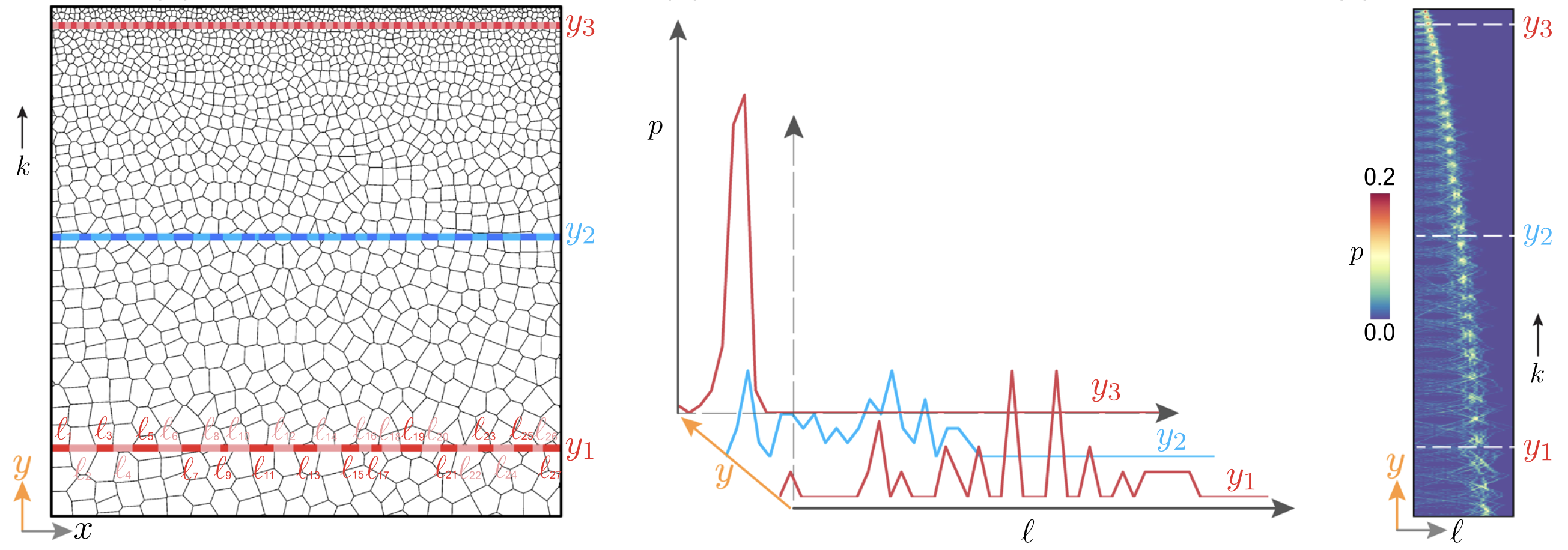
I developed SR-CLD (spatially-resolved chord length distributions) as an efficient method for quantifying and visualizing spatial heterogeneity in complex microstructures. Using a scan-line algorithm to capture directional variations in constituent sizes, SR-CLD provides detailed, high-resolution statistical descriptions of non-uniform materials across simulated and experimental datasets.

Automated Segmentation

I developed a hybrid, machine learning–assisted approach for large-scale segmentation and spatial analysis of melt pools in complex 3D printed metal parts. By combining limited human annotation with automated segmentation and using chord length distribution (CLD) as a robust metric of melt pool size, this method enables efficient, scalable, and statistically reliable characterization of additive manufacturing artifacts.

Acknowledgements

I acknowledge the support by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-2137419. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the National Science Foundation.